今回から平面走査法という手法による、
はじめに
計算幾何学では、
多数の線分から交差を見つける
前回、
さて今後、
線分の交差を示すクラス
まず初めに、
public class Intersection {
public LineSegment segment1;
public LineSegment segment2;
public Intersection(LineSegment segment1, LineSegment segment2) {
this.segment1 = segment1;
this.segment2 = segment2;
}
public Point2D getIntersectionPoint() {
return segment1.getIntersectionPoint(segment2);
}
@Override
public String toString() {
return segment1 + " : " + segment2;
}
}さて、
ここでは、
@Override
public boolean equals(Object obj) {
if (obj == this) {
return true;
} else if (obj instanceof Intersection) {
Intersection other = (Intersection) obj;
// segment1とsegment2を交換しても同値性が変わらないようにする
if (segment1.equals(other.segment1) && segment2.equals(other.segment2)) {
return true;
} else if (segment1.equals(other.segment2) && segment2.equals(other.segment1)) {
return true;
}
}
return false;
}
@Override
public int hashCode() {
// segment1とsegment2を交換してもハッシュ値が変わらないようにする
return segment1.hashCode() + segment2.hashCode();
}交差検出のインターフェース
次に、
public interface IntersectionDetector {
Collection<Intersection> execute(List<LineSegment> segments);
}総当たり法による交差検出
では、
この総当たり法を実装したものが、
public class BruteForceIntersectionDetector implements IntersectionDetector {
public Collection<Intersection> execute(List<LineSegment> segments) {
List<Intersection> result = new ArrayList<Intersection>();
int size = segments.size();
for (int i = 0; i < size; i++) {
LineSegment s1 = segments.get(i);
// j < iの場合は調査済み、またj = iの場合は2線分が同一となり交差を調べる
// 必要がないため、j = i + 1からループを開始する
for (int j = i + 1; j < size; j++) {
LineSegment s2 = segments.get(j);
if (s1.intersects(s2)) {
result.add(new Intersection(s1, s2));
}
}
}
return result;
}
}コードを見ると分かるように、
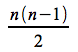
回の交差判定が行われることになります。この計算量は
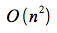
となります。
線分の数が少ないうちは、
そんなに多くの線分を扱うケースなんてあるの?

さらに、
平面走査法
総当たり法のどこに無駄があるのか、
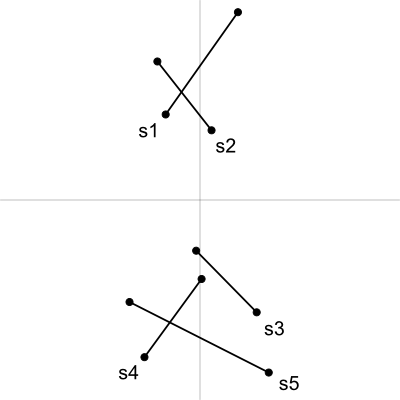
こうした線分同士の
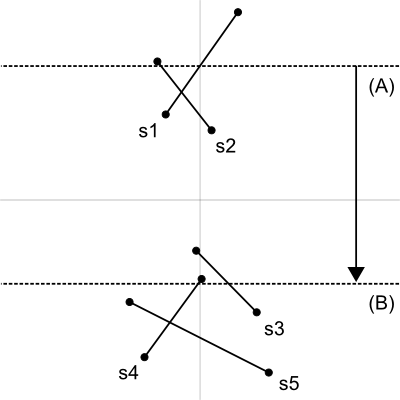
平面走査法では、
平面走査法の具体的な実装については、
まとめと次回予告
今回は、
今回作成したプログラムのソースコードがダウンロードできます。
- 第3回ソースコードファイル
(gihyo-geometry-part3. zip/ Zip圧縮/約50KB)
次回は、



